 W-54 Davy Crockett (38 K)
W-54 Davy Crockett (38 K)




By Carey Sublette
Last changed 18 May 2002
It is impossible to verify at the time of this writing whether nuclear devices sized to fit in side a suitcase were actually manufactured by the former Soviet Union, as alleged by Alexander Lebed in September 1997. It is certainly possibel to assess the technicial plausibility of such a claim and to provide a analysis of the likely characteristics of the weapons Lebed described.
A suitcase bomb with dimensions of 60 x 40 x 20 centimeters is by any standard a very compact nuclear weapon. Information is lacking on compact Soviet weapons, but a fair amount of information is available on compact US designs which provides a good basis for comparison.
The smallest possible bomb-like object would be a single critical mass of plutonium (or U-233) at maximum density under normal conditions. An unreflected spherical alpha-phase critical mass of Pu-239 weighs 10.5 kg and is 10.1 cm across.
A single critical mass cannot cause an explosion however since it does not cause fission multiplication, somewhat more than a critical mass is required for that. But it does not take much more than a single critical mass to cause significant explosions. As little an excess as 10% (1.1 critical masses) can produce explosions of 10-20 tons. This low yield seems trivial compared to weapons with yields in the kilotons or megatons, but it is actually far more dangerous than conventional explosives of equivalent yield due to the intense radiation emitted. A 20 ton fission explosion, for example, produces a very dangerous 500 rem radiation exposure at 400 meters from burst point, and a 100% lethal 1350 rem exposure at 300 meters. A yield of 10-20 tons is also equal to the yield of the lowest yield nuclear warhead ever deployed by the US -- the W-54 used in the Davy Crockett recoilless rifle.
A mere 1.2 critical masses can produce explosive yield of 100 tons, and 1.35 critical masses can reach 250 tons. At this point a nation with sophisticated weapons technology can employ fusion boosting to raise the yield well into the kiloton range without requiring additional fissile material.
The amount of fissile material that constitutes a "critical mass" varies with the material density and the type of neutron reflector present (if any). A high explosive implosion can compress fissile material to greater than normal density, thus reducing the critical mass. A neutron reflector reduces neutron loss and reduces the critical mass at a constant density. However generally speaking, adding explosives or neutron reflectors to a core adds considerably more mass to the whole system than it saves.
A limited exception to this is that a thin beryllium reflector (thickness no more than the core radius) can actually reduce the total mass of the system, although it increases its overall diameter. For beryllium thicknesses of a few centimeters, the radius of a plutonium core is reduced by 40-60% of the reflector thickness. Since the density difference between these materials is on the order of 10:1, substantial mass savings (a couple of kilograms) can be achieved. At some point though increasing the thickness of the reflector begins to add more mass than it saves since volume increases with the cube of the radius. This marks the point of minimum total mass for the reflector/core system.
A low yield minimum mass or minimum volume weapon would thus use an efficient fissile material (plutonium or U-233), a limited amount of high explosives (sufficient only to assembly the core, not to compress it to greater than normal density), and a thin beryllium reflector.
We can now try to estimated the absolute minimum possible mass for a bomb with a significant yield. Since the critical mass for alpha-phase plutonium is 10.5 kg, and an additional 20-30% of mass is needed to make a significant explosion, this implies 13 kg or so. A thin beryllium reflector can reduce this by a couple of kilograms, but the necessary high explosive, packaging, triggering system, etc. will add mass, so the true absolute minimum probably lies in the range of 11-15 kg (and is probably closer to 15 than 11).
This is probably a fair description of the W-54 Davy Crockett warhead. This warhead was the lightest ever deployed by the US, with a minimum mass of about 23 kg (it also came in heavier packages) and had yields ranging from 10 tons up to 1 Kt in various versions. The warhead was basically egg-shaped with the minor axis of 27.3 cm and a major axis of 40 cm. The test devices for this design fired in Hardtack Phase II (shots Hamilton and Humboldt on 15 October and 29 October 1958) weighed only 16 kg, impressively close to the minimum mass estimated above. These devices were 28 cm by 30 cm.
The W-54 design probably approaches the minimum size for a spherical implosion device (the US has conducted tests of a 25.4 cm implosion systems however).
The W-54 nuclear package is certainly light enough by itself to be used in a "suitcase bomb" but the closest equivalent to such a device that US has ever deployed was a man-carried version called the Mk-54 SADM (Small Atomic Demolition Munition). This used a version of the W-54, but the whole package was much larger and heavier. It was a cylinder 40 cm by 60 cm, and weighed 68 kg (the actual warhead portion weighed only 27 kg). Although the Mk-54 SADM has itself been called a "suitcase bomb" it is more like a "steamer trunk" bomb, especially considering its weight.
Minimum mass and minimum volume are not the only design criteria of interest of course, since even 25.4 cm (10 inches) is rather thick even for a suitcase and is wider than the reported 20 cm thickness of Alexander Lebed's suitcase bomb. Another approach is to instead develop a minimum diameter or minimum thickness design.
Minimizing nuclear weapon diameters has been a subject of intense interest for developing nuclear artillery shells, since the largest field artillery is typically the 208 mm (8.2 inch) caliber, with 155 mm (6.1 inches) artillery being the workhorse. Nuclear artillery shell designs with diameters as small as 105 mm have been studied. Packaging a nuclear artillery shell in a suitcase is an obvious route for creating a compact man-portable device.
The US has developed several nuclear artillery shells in the 155 mm caliber. The only one to be deployed was the W-48 nuclear warhead developed by UCRL, packaged in the M-45 AFAP (artillery fired atomic projectile) shell. The W-48 nuclear warhead measured 86 cm (34") long and weighed 53.5-58 kg (118-128 lbs). Its yield was on the order of 70 to 100 tons (it was tested in the Hardtack II Tamalpais shot with a yield of 72 tons, predicted yield was 100-300 tons).
The smallest diameter US test device publicly known was the UCRL Swift device fired in the Redwing Yuma shot on 28 May 1956 . It had a 5" (12.7 cm) diameter, a length of 62.2 cm (24.5 inches) and weighed 43.5 kg (96 lb). The test had a yield of 190 tons, but was intended to be fusion boosted (and thus would probably have had a yield in the kiloton range) but its yield was insufficient to ignite the fusion reaction and it failed to boost in this test. This test may have been a predecessor to the W-48 design.
Later and lighter 155 mm designs were also developed -- the W74 (canceled early in development), and the W-82/XM-785 shell. The W82 had a yield of up to 2 kilotons and weighed 43 kg (95 lb), but included a number of sophisticated additional features within this weight. Since it was capable of being fielded with a "neutron bomb" (enhanced radiation) option, which is intrinsically more complex than a basic nuclear warhead, and was in addition rocket boosted, the actual minimum nuclear package was substantially lighter than the weight of the complete round. Its overall length was 86 cm (34").
It is reported that designs least as small as 105 mm (4.1 inches) are possible. A hypothetical 105 mm system developed for use in an artillery shell would be about 50 cm (20 inches) long and weigh around 20 kg.
Compact nuclear artillery shells (208 mm and under) are based on a design approach called linear implosion. The linear implosion concept is that an elongated (football shaped) lower density subcritical mass of material can be compressed and deformed into a critical higher density spherical configuration by embedding it in a cylinder of explosives which are initiated at each end. As the detonation progresses from each direction towards the middle, the fissile mass is squeezed into a supercritical shape. The Swift device is known to have been a linear implosion design.
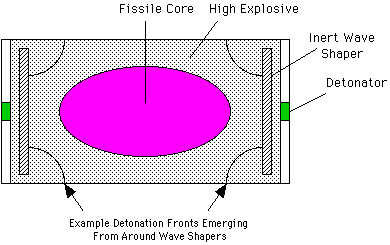
It is quite likely, that should the suitcase bombs described by Lebed actually exist, that they would use this technology. It is clear that any of the 155 mm artillery shells, if shortened by omitting the non-essential conical ogive and fuze would fit diagonally in the package that Lebed describes, and the Swift device would fit easily. If the yield is as much as 10 kilotons, then the device would have to be fusion boosted.
A somewhat more sophisticated variation would extend the linear implosion concept to cylindrical implosion, in this case an oblate (squashed) spheroid, roughly discus-shaped, of plutonium would be embedded in a cylinder of high explosive which is initiated simultaneously around its perimeter. The cylindrically converging detonation would compress and deform the fissile mass into a sphere, that could be wider than the original thickness of the system. This type of design would make the flattest possible bomb design, perhaps as little as 5 cm. The only obvious application for such a device would be briefcase bomb, and would require a special development effort to create it.
See Section 4.2 of the Nuclear Weapons FAQ for more details.
Source of weapon and test details The Swords of Armageddon, by Chuck Hansen, Chuckelea Publishing, 1995.